Unfortunately somehow only Jim Cramer has mentioned the Parabolic PDE that I had tweeted about to my colleagues who I routinely showboat for. It seems as though there was an unwillingness to assume a corollary but he did insinuate he understood the concept that the underlying financial were to be again tested; but the point at which he made that final observation was at
That is to say that I will independently tap into my Mega Society/Loser Status because financial power rules the world and not mediocre insecure teachers or unsympathetic pupils. This is purely for the benefit of myself with the aforementioned time parameter left undefined because I surely wont be compensated for a corollary; I will revisit this function when I get to enjoy writing the proof after the corollary has been proven, although the derivation is just as valid as a proof thereby self evident as in my other examples. I should also admit that the taylor polynomials are fairly discreet and their vector values are private and I am unwilling to disclose them until the day before a trade so as to ensure their trivial positions in the grand scheme of Jim Cramers unattainable Taylor Polynomial vector pool, and the parabolic effects of quality analysis that I have put forth is not again questioned but as constant as force.
The financial power is actually a triumvirate of Mathematical Physics and not an effervescent joker without the ability to prove how he could liquidate anyones said holdings anyone.
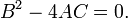A.K.A. Controlled Diffusion Perimeter (d" of )
- My Foretasted stress ranges and Individual Stock "Outliers" although BAC, JPM, CVX, and OGZPY.PK are as much an outlier as any stock I analyze. A.K.A. Hamiltonian-Jacobi "Pools"
- Random Walk which is what Jim Cramer refers to as an "Outlier," but when you can precisely ameliorate the pools into Stochastic Control(Hamiltonian-Jacobi Pools) and Deterministic Control of the Controlled Diffusion Perimeter
How is this possible? There isn't any collar or hedge to describe to a worldy financier, the point is a parabola construction is the way to factor price spreads which become positive when both buyers and sellers participate.
A hypotenuse can be triangulated from any probability space within the Controlled Diffusion Perimeter (d" of )
So when I say there is an inversion at the Ses basis I would agree with Jim Cramer that this Bulls and Bears and April and May talk doesn't apply because the price action won't allow for anything after a jounce, so it remains the level set method at chain velocity. So when I allude to Dionýz Ilkovič and Heyrovský's Polarograph and DME you can be sure you can either disprove me or agree with my train of thought. In fact I recalled as solution to the confabulation or the apparent lack of depth and applications refuting no solution for diffusion properties. http://www.bloomberg.com/news/2012-04-08/fda-for-derivatives-won-t-defuse-wall-street-s-bombs.html
Again I wish no disdain for the ilk to which Jim Cramer or William D. Cohan belong but I recalled the solution as it was directly related to not only my past solutions for the types of market problems that are shared by Mr. Cohan and Mr. Cramer. The only problem here is I have no one to say to me you are correct for I am a physicist, a Chemical Engineer, or a Mathematician. Once the connection has been made between my device and the market I would seriously consider using Vector Pools to isolate and remove any further competition.
That is the to say the inversion is now positive as it was before, and Parabolic PDE's should not be confused with exponential equations because random walks for distinct stochastic constructs measured by triangles and other geometric shapes and not cycles. Think Benoît Mandelbrot.
Taylor Gang!
http://en.wikipedia.org/wiki/Taylor_polynomial
No comments:
Post a Comment